CB 3.16-3.17 Simulations • 22 min read

3.16 Simulations

Part 1

Learning Objective:

• How computers can be used to represent real-world phoenomena

Essential Knowledge:

• Simulations are abstractions for more complex objects or phoenomena for a specific purpose

• Mimic real-world events, with simplification

• Made to refine results/hypothesis

• May have limitations or bias

• When creating car-testing simulations, we assume the driver is at least 16 years old, and has their seatbelt on.

• Examples: Radar displays, RNG simulating variability, and weather forecasting

Flight Simulator

• Flight Simulator is an example of a simulation
• It simulates flying real planes anywhere you want
  • You are able to choose your type of plane
  • You can fly anywhere you want
• Flight simulator is benefical in saving money, time, and resources because:
  • No risk of damaging a real plane
  • No risk of risking life of passengers or valuable crew members
  • No waste of resources like gas and fuel
  • Practically no money
• Siomulations like flight simulator save a lot of money and resources but may be negative in the fact that it isn’t acutally real life.

Vocab:

• Simulation Abstraction - The little errors or unusual things that come up when running a simulation

Popcorn Hack 1:

• True or false:

1. (T or F) A simulation will always have the same result

2. (T or F) A simulation is used when it would be more convenient than an experiment

3. (T or F) A simulation models very specific scenarios

4. (T or F) A simulation cannot provide valid data to be used as fact

Answers

Part 2

• Simulations are abstractions; mocking the real world items to get an idea of how they work on actual items

Simulations vs. Experiments:

Simulations	Experiments
Simulations are where you try to mock the real-world items to get an idea of how they may perform without having to use the actual items.	Experiment is dealing with an actual real-world object, using real-world equipment.
Simulations can be less expensive than experiments.	Experiments can be more expensive than simulations.
Simulations provide estimated results based on models.	Experiments provide actual results.
A simulation can model real-world events that are not feasible or doable for experiments.	Experiments may not be possible using real-world equipment, for reasons such as the assets are not available, or they would be too dangerous.
Simulations are easier to repeat.	Once set up, simulations may be faster and Experiments may take a long time to set up and conduct.
Simulations can be safer to conduct. Example: Simulation of a car crash	Experiments can provide results that prove the safety of the product or event. Example: Flying an aircraft prototype.

• Simulations are less risky and provide information on the probability of something happening
• Experiments are riskier but more invasive, allowing for results
• Simulations are less expensive
• EXAMPLE: Tony Stark’s time travel SIMULATION was a test to see if his time travel theory would work
• EXAMPLE RESULT: Tony Stark’s time travel SIMULATION worked and it provided an accurate estimate of how it would work. He then proceeded with an EXPERIMENT to see if it would actually work.

Popcorn Hack 2:

Which of the following scenarios is better to do as a simulation than a calculation?

1. Keeping score at a football game
2. Studying the spread of disease in a country
3. Determining average grade from a set of quizzes
4. Studying the impact carbon emissions on the environment

Popcorn Hack 3:

Which of the following statements expresses a constraint of using a computer simulation to imitate a real-world object or system?

1. Computer simulations can only be done after the real-world object or system has been created.
2. Computer simulations can only run-on powerful computers that are not accessible to the public.
3. Computer simulations usually make some assumptions about the real-world object or system being modeled.
4. Computer simulations parameters and conditions are difficult to change.

Simulations Overview

• Simulations can contain bias derived from the choices of real-world elements that were included or excluded.
• Simulations are most useful when real-world events are impractical for experiments (e.g., too big, too small, too fast, too slow, too expensive, or too dangerous).
• Simulations facilitate the formulation and refinement of hypotheses related to the objects or phenomena under consideration.
• Random number generators can be used to simulate the variability that exists in the real world.

3.17 Algorithmic Efficiency

Part 1

What is Algorithmic Efficiency ?

• A way to find the fastest and least resource dependent solution to a problem
• Measures using number of computations (you can think of them as steps) in a algorithm before you can solve your problem
• Generally speaking less computations = faster = better code but it’s heavily dependent on input size as algorithms with small input sizes may sometimes seem faster but are actually much slower at high input sizes

Basic Algorithm Example:

• Picture a set of 4 cards numbered [4,6,7,2]. To sort these cards algorithmically, you run through them from left to right, comparing if the numbers are bigger or smaller than the card to their right.
• If they’re already ordered correctly, you keep them as is and mark down that you made a comparison. If they’re bigger than the card on their right, you swap their positions and repeat the process for the next set of 2 cards, until you fixed them entirely. You mark down comparisons and swaps throughout the algorithm.
• For this example, you have to make 7 comparisons and 3 swaps to make the list ordered, into [2,4,6,7], even though you’re only actually changing the position of one number.

Better Algorithm Example:

• A different algorithm for the same problem, for example, one where you instead hold onto the smallest card instead each time you go through the set, could only use 6 comparisons and 1 swap, making it algorithmically more efficient.

Popcorn Hack 4

Which algorithm in this set is unreasonable and why?

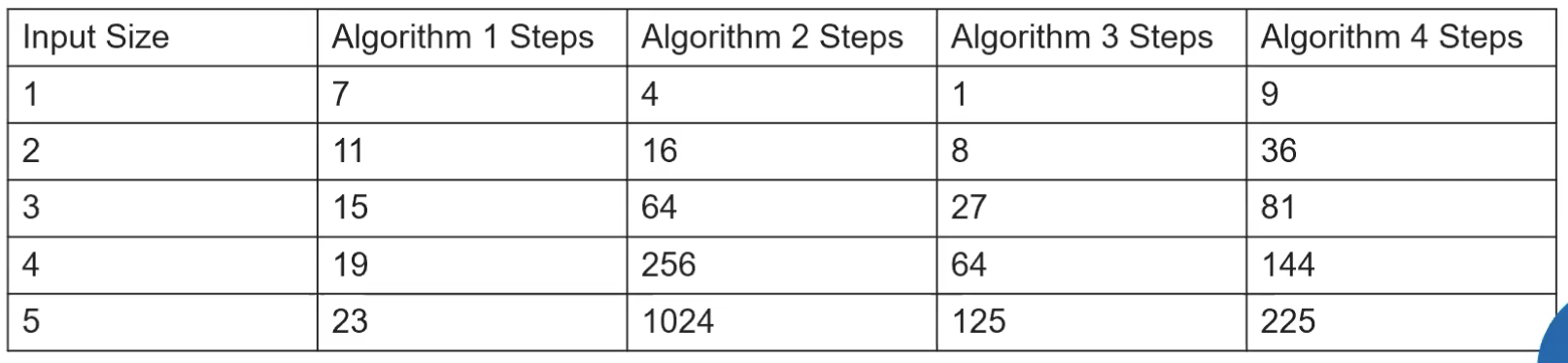
Algorithm Efficiency Simply Explained:

• On the most basic level, you can think of efficiency as a measure of the number of steps it takes you to reach your answer. If one algorithm has 7 total steps and a different one for the same problem has 20, your first algorithm is likely more efficient.
• But, when analyzing algorithm efficiency, you can only achieve accuracy by measuring with different input sizes as well. This is due to the fact that some algorithms increase their number of steps with polynomial efficiency (linear increasing or other polynomial styles), but others increase exponentially or factorially.
• Algorithms are only reasonable if their operate with polynomial efficiency

Part 2

Key Term

• A heuristic is an approach to a problem where it’s solution is not optimal but used because other techniques that WILL find the best solution are not practical.

Traveling Salesperson Problem

• There is a set of cities. Find the shortest route that visits every city exactly once and returns to the start point

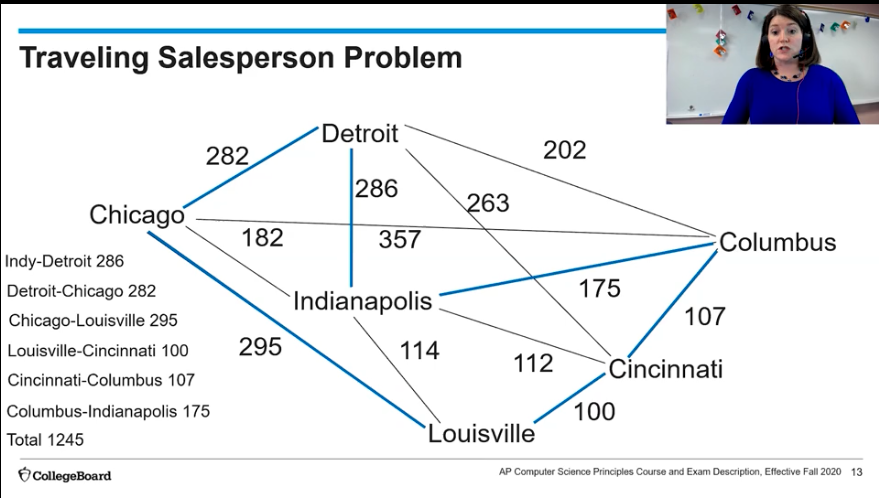
• Picked randomly
• Imagine finding the shortest route with 100+ cities

• Take into account the time it takes

• Instead of trying every single route, use a heuristic
  • A heauistic might not give the best possible solution, but it will have a solution in a reasonable amount of time

Traveling Sales Problem: Nearest Neighbor

• In the traveling salesperson problem, traveling to the nearest neighbor will give a solution
• It isn’t the best solution but it is optimal and saves time.

Popcorn Hack 4

Example Algorithm

• This is an example algorithm using the nearest neighbor method for the Traveling Salesperson Problem

def nearest_neighbor_tsp(distances):
    num_cities = len(distances)
    unvisited_cities = list(range(num_cities))
    tour = [unvisited_cities.pop(0)]  # Start with the first city

    while unvisited_cities:
        current_city = tour[-1]
        nearest_city = min(unvisited_cities, key=lambda city: distances[current_city][city])
        tour.append(nearest_city)
        unvisited_cities.remove(nearest_city)

    # Return to the starting city
    tour.append(tour[0])

    total_distance = sum(distances[tour[i]][tour[i + 1]] for i in range(num_cities))

    return tour, total_distance

# Example usage
distances = [
    [0, 29, 20, 21],
    [29, 0, 15, 17],
    [20, 15, 0, 28],
    [21, 17, 28, 0]
]

optimal_tour, min_distance = nearest_neighbor_tsp(distances)
print("Optimal Tour:", optimal_tour)
print("Total Distance:", min_distance)

Optimal Path: (0, 2, 1, 3)
Minimum Distance: 73

Homework Hacks

1. Write an algorithm in python that uses a function to sort 4 numbers from lowest to highest.
2. What are 3 benefits and 1 negative of using a simulation
3. Think of social media platforms that you go on. What is an aspect of one of those platforms that uses an algorithm to improve their feature and usability?

##